La prossima cosa che dobbiamo capire è come definire la velocità di 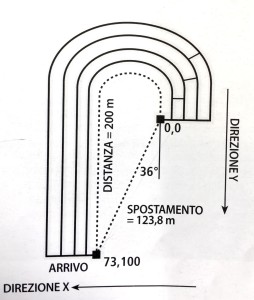movimento di un individuo.

Quanto velocemente un atleta ha percorso i 200 m?

Possiamo determinare quanto velocemente un atleta ha corso (media sull’intera distanza dei 200 m) dividendo quanto velocemente per quanto lontano, ma il valore che otteniamo dipende da come consideriamo il quanto velocemente, se lo consideriamo una grandezza scalare oppure vettoriale

– Se vogliamo conoscere la velocità del movimento sulla distanza totale dei 200 m, calcoleremo la velocità come una grandezza scalare:

velocità scalare(speed)= Δd÷Δt o Δd/Δt
 ("Δ" indica variazione di, e "Δt" indica intervallo temporale)

– Se invece vogliamo conoscere quanto velocemente e in che direzione risultante si sia mosso l’atleta, calcoleremo la velocità come grandezza vettoriale:

velocità vettoriale (velocità) (v) =Δs÷Δt, Δs/Δt, lungo una data direzione (cioè, lo spostamento (s) nell'intervallo temporale)

C’è, dunque, una grande differenza se la velocità viene calcolata come scalare o vettoriale.

In alcuni casi è più utile calcolare la velocità vettoriale.

– Se un triatleta nuota per 1,5  km attraverso un lago, ciò che interessa è il tempo impiegato per percorrere tale distanza, anche se magari l’atleta perde la direzione e percorre una distanza totale di 2 km per completare la gara!
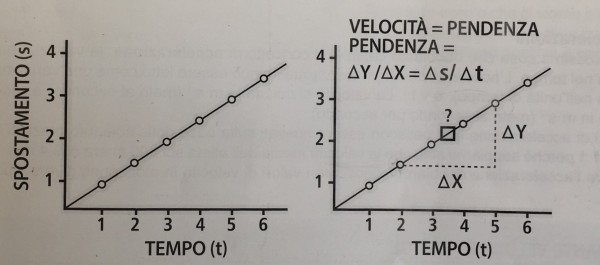
Esiste anche un altro metodo, più avanzato, per calcolare la velocità vettoriale. Come puoi vedere, calcolando la velocità tra due istanti temporali, quella che si ottiene è solo la velocità media. Possiamo, però, stimare la velocità istantanea, utilizzando procedure matematiche più precise. La velocità istantanea viene calcolata su un intervallo di tempo molto breve (vicino a zero). Considera il grafico qui sotto (fig.2) di un oggetto che si muove a velocità costante. Puoi vedere che l’oggetto si muove di 0,5 unità al secondo. Possiamo quindi calcolare la velocità utilizzando l’equazione della velocità media come mostrato nel grafico a destra:

(3-1,5)/(5-2) = 1,5/3=0,5 unità al secondo

Hai notato che in realtà abbiamo calcolato la pendenza (il coefficiente angolare) di questa retta, o il rapporto tra “la variazione verticale e quella orizzontale”? Questo suggerisce che se possiamo calcolare la pendenza di una linea in un fato punto, possiamo calcolare la velocità istantanea.

Fig. 1.2.
La velocità di un oggetto in ogni istante è uguale alla pendenza (al coefficiente angolare) della relazione tra spostamento e tempo.

I dati di spostamento in funzione del tempo per questo oggetto sono ben descritti da una linea retta.
Probabilmente ti ricordi che l’equazione di una retta è:

y=ax+b, dove a è la pendenza (il coefficiente angolare) della retta e b è l'intercetta sull'asse delle y (il punto in cui la retta interseca l'asse y o verticale).

Quindi, equazione relativa ai nostri dati corrisponde a:

y=0,5+0, perché la pendenza (o coefficiente angolare è di 0,5 unità al secondo e la retta interseca l'asse y al punto 0.

In questo esempio è facile osservare come la pendenza (costante, nel caso di una retta) sia di 0,5 unità al secondo e quindi la velocità sia pari a 0,5 unità al secondo.

Puoi anche notare che la pendenza è uguale alla derivata di questa funzione. Chi ha un pò di familiarità con la matematica, ricorderà che per trovare la derivata di una retta, dove N sia il termine di potenza per x, bisogna moltiplicare N per x alla potenza di N-1, quindi 0,5+0 diventa

(0,5 ∗ 1) ∗(xˆ(1-1)) + (0∗0) ∗ xˆ(1-1) 
(0,5x in realtà corrisponde a 0,5xˆ1

= 0,5∗1 + 0
= 0,5

Questo metodo ha ancora più significato quando abbiamo una curva della velocità più complessa.
Per esempio, se l’equazione della curva fosse

3xˆ2+5x+7
si avrebbe che:
(3∗2)∗xˆ(2-1)+(5∗1)∗xˆ(1-1)+(7∗0)∗xˆ(0-1)
=6x+5

Dunque, se ti chiedessi quale fosse la velocità al tempo = 3,2s, dovresti inserire 3,2 nell’equazione al posto della x (ricorda che il tempo è rappresentato sull’asse delle x) e il risultato sarebbe che la velocità = 19,2 + 5= 24,2 metri al secondo.

Possiamo supporre che lo spostamento sia stato misurato in metri, quindi che la velocità è di 24,2 m∗sˆ-1.
Se conosci l’equazione che mettono in relazione lo spostamento con il tempo (o almeno la parte della curva che ti interessa), puoi calcolare la velocità istantanea.
Se le tue conoscenze di matematica non sono buone, può apparire un pò complicato ma è importante che tu capisca l’idea alla base di questo ragionamento (cioè, che si può determinare la pendenza di una linea in un punto specifico).

Ti può anche interessare:
Parte Prima:”Ti sei ma chiesto chi vincerà una gara di corsa dei 200 metri ? l’atleta con la maggiore accelerazione iniziale o l’atleta che raggiunge la velocità massima più alta?”

Parte terza|Accellerazione: “Ti sei ma chiesto chi vincerà una gara di corsa dei 200 metri ? l’atleta con la maggiore accelerazione iniziale o l’atleta che raggiunge la velocità massima più alta?”

Parte quarta: la direzione del movimento|Come descrivere la direzione di movimento : “Ti sei ma chiesto chi vincerà una gara di corsa dei 200 metri ? l’atleta con la maggiore accelerazione iniziale o l’atleta che raggiunge la velocità massima più alta?”

Parte quinta| La risposta|Come descrivere la direzione di movimento : “Ti sei ma chiesto chi vincerà una gara di corsa dei 200 metri ? l’atleta con la maggiore accelerazione iniziale o l’atleta che raggiunge la velocità massima più alta?”